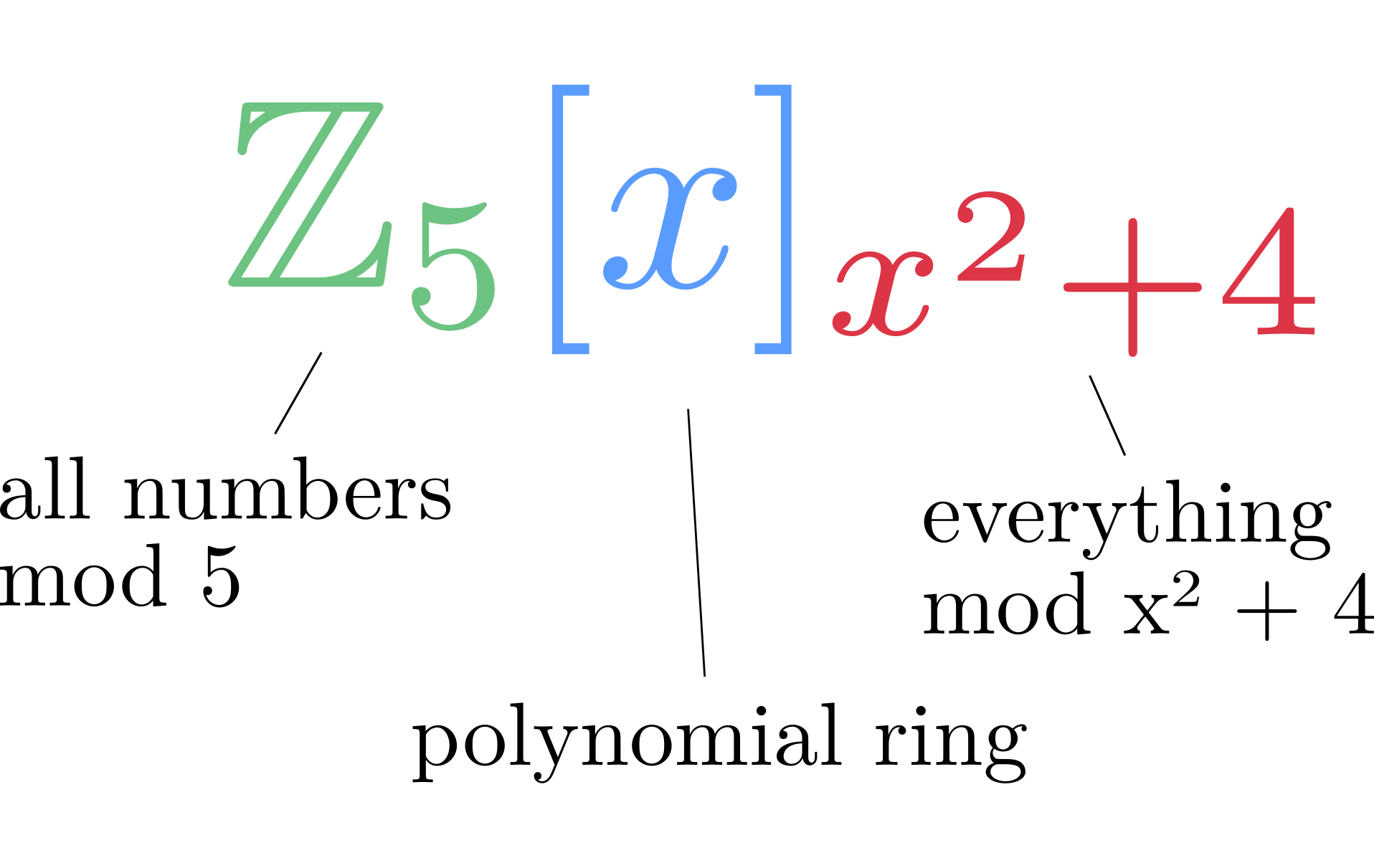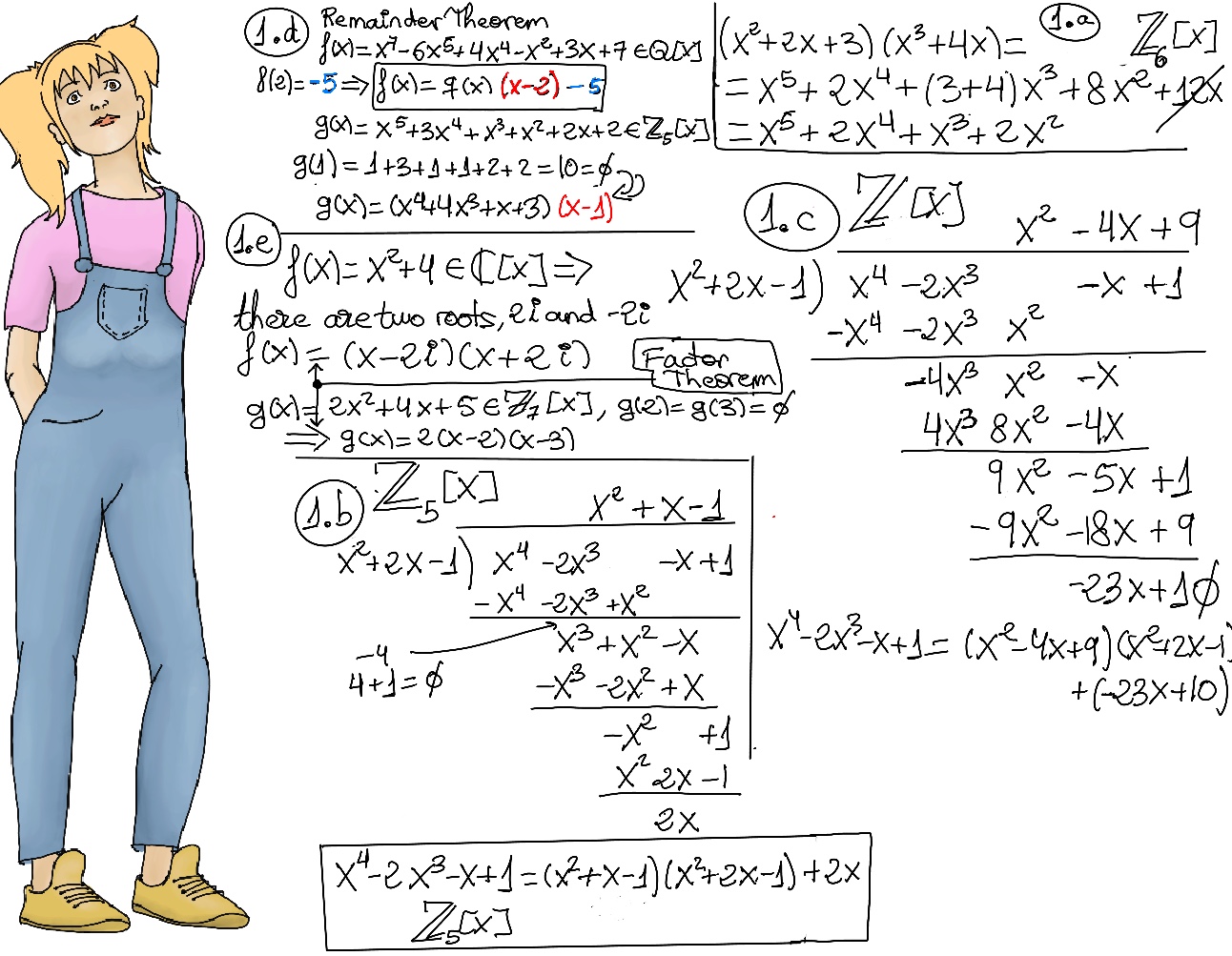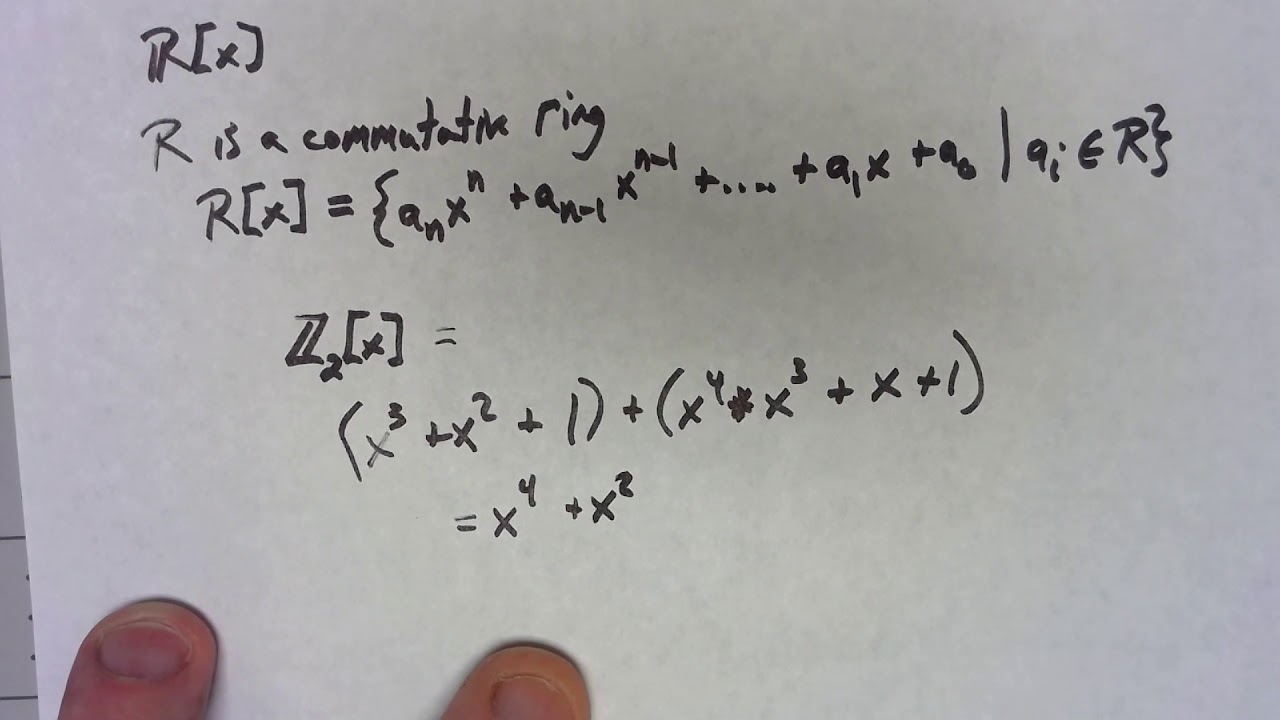abstract algebra - Visualizing quotient polynomial rings are fields for maximal ideals which are generated by irreducible monic - Mathematics Stack Exchange
abstract algebra - Trying to understand a proof for the automorphisms of a polynomial ring - Mathematics Stack Exchange
RNT2.5. Polynomial Rings over Fields - YouTube
![Figure A.1. Relationships among the polynomial ring F[D], the ring... | Download Scientific Diagram](https://www.researchgate.net/publication/265308291/figure/fig4/AS:669571732226054@1536649749280/Figure-A1-Relationships-among-the-polynomial-ring-FD-the-ring-FD-of-formal-power.png "Figure A.1. Relationships among the polynomial ring F[D], the ring... | Download Scientific Diagram")
Figure A.1. Relationships among the polynomial ring F[D], the ring... | Download Scientific Diagram
![SOLVED: For two polynomials f(z) and g(x) in the polynomial ring @[kz], the following steps of the Euclidean algorithm have been given: f(z) = q(c)g(z) + f(z), 0 < deg(fi(z)) < deg(g(z)),](https://cdn.numerade.com/ask_images/a2bf060bef6942368f076a34f722b7aa.jpg "SOLVED: For two polynomials f(z) and g(x) in the polynomial ring @[kz], the following steps of the Euclidean algorithm have been given: f(z) = q(c)g(z) + f(z), 0 < deg(fi(z)) < deg(g(z)),")
SOLVED: For two polynomials f(z) and g(x) in the polynomial ring @[kz], the following steps of the Euclidean algorithm have been given: f(z) = q(c)g(z) + f(z), 0 < deg(fi(z)) < deg(g(z)),
abstract algebra - polynomial ring over finite field - Mathematics Stack Exchange
abstract algebra - Algorithm for inversion in truncated polynomial ring - Mathematics Stack Exchange
![6.6 Rings and fields Rings Definition 21: A ring is an Abelian group [R, +] with an additional associative binary operation (denoted ·) such that. - ppt download](https://images.slideplayer.com/34/10171857/slides/slide_4.jpg "6.6 Rings and fields Rings Definition 21: A ring is an Abelian group [R, +] with an additional associative binary operation (denoted ·) such that. - ppt download")
6.6 Rings and fields Rings Definition 21: A ring is an Abelian group [R, +] with an additional associative binary operation (denoted ·) such that. - ppt download
When is a polynomial ring a field? | xyquadrat.ch
Polynomial Rings. Principal ideal domains | JustToThePoint
Group Theory 69, Polynomial Rings - YouTube
Abstract Algebra 14.5: Introduction to Polynomial Rings - YouTube
Polynomial Ring - Definition And Proof- Euclidean Domain - Lesson 13 - YouTube
Chapter 2 Factorization in Polynomial Rings
Chapter 7 Polynomial Rings 7.1 Polynomials
Abstract Algebra | Polynomial Rings - YouTube
PDF) Some Algebraic Properties of Polynomial Rings
Solved 5. In the polynomial quotient ring defined on slide | Chegg.com
Ring of Polynomials, Ideal in a Ring & Cyclic Code - YouTube
abstract algebra - Help to understand the ring of polynomials terminology in $n$ indeterminates - Mathematics Stack Exchange
Polynomial Rings, Lecture Notes- Maths - Prof Michael Vaughan Lee | Study notes Mathematics | Docsity
The Algebra of Polynomial Rings - YouTube
Polynomial Rings (CHAPTER II) - Rings and Ideals
Solved Let R be a commutative ring with 1. Let M₂ (R) be the | Chegg.com
